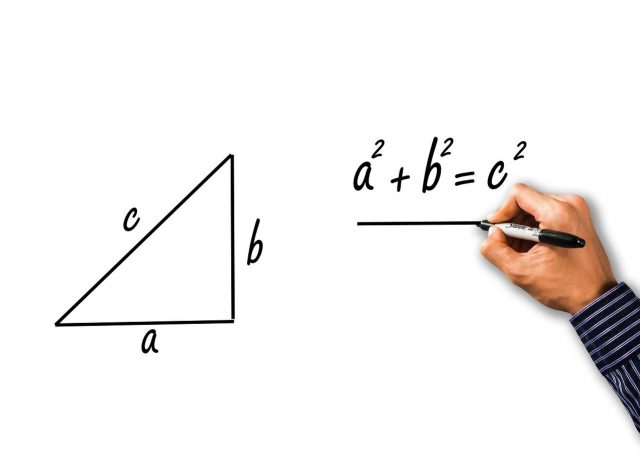
Geometry is that branch of mathematics which is primarily concerned with questions of shape, size, the relative position of figures, and the properties of space. Geometry helps to measure different shapes, for example, the area of triangle with 3 sides formula can be used to find the area of a triangle with a very useful formula, and in this article, we will see how it is calculated. A variety of possible shapes are defined by geometry and one of the most common shapes which is possible using the minimum number of three straight lines is a triangle.
For any geometrical shape, there are two main ways to measure its size. These two measures commonly employed are Area and Perimeter. While the area of a shape tells about how much surface the shape covers, the perimeter of a shape helps quantify how long the periphery of the shape is.Further, if you want to find out more about Geometry starting from the basics, then please visit cuemath.com.
For a triangle, which is a shape made by the intersection of three straight lines at three different points, we can use geometry to calculate the area and its perimeter quite easily. It is very useful to use geometry to find out area and perimeter due to its usage in day-to-day life.
The area of a triangle can be found out in many different ways; for some of the triangles, it can be easier than others to calculate the area and perimeter because of the specific properties related to that specific type of triangle. So let us have a quick dive into the different types of triangles.
Triangles are divided into different types based on how regular or irregular they are. Examples of regularity would be the equilateral triangle, wherein all the three sides of the triangle are equal. Keep in mind that if three sides of the triangle are equal, then the three interior angles of the triangle would also be equal, and using the fundamental theorem defining triangles, that is the sum of all three interior angles of a triangle is 180 degrees, we can deduce that measure of each angle would be 180 divided by three that is 60 degrees.
To calculate the area of an equilateral triangle, the formula hence is very straightforward.
Area of an equilateral triangle = (√3/ 4 ) x (side of an equilateral triangle)². Or an isosceles triangle in which two sides of the triangle are equal.
But in the case of a normal triangle in which all the three sides are of unequal lengths, then the formula to calculate the area of such a triangle is in two steps.
Step number one is to calculate the semi perimeter of the triangle; the semi-perimeter of a triangle is the perimeter of the triangle divided by two. So, if the triangle has sides of lengths a, b, and c, then the semi-perimeter of the triangle would be (a + b + c)/2 = s (semi-perimeter of a triangle with sides a, b and c).
Next step number two is to use the semi-perimeter of the triangle denoted by ‘s’ in the formula
√[s(s-a)(s-b)(s-c)] = Area of a triangle
This formula for the area of the triangle is called Heron’s formula.
It is important to remember this formula requires regular practice involving many problems, and for that, a geometry worksheet that compiles a series of problems involving mathematical calculations and angles would be useful. Fortunately, there are loads and loads of free geometry worksheets available online for you to tackle your learning goals head-on.
These free geometry worksheets will help you practice the area of a triangle with 3 sides, the area of a circle, the area of a square, and the area of a triangle. Visit Cuemath for more such worksheets on geometry.












